1335. Minimum Difficulty of a Job Schedule

You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the i-th job, you have to finish all the jobs j where 0 <= j < i).

You have to finish at least one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the d days. The difficulty of a day is the maximum difficulty of a job done in that day.

Given an array of integers jobDifficulty and an integer d. The difficulty of the i-th job is jobDifficulty[i].

Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.

Example 1:

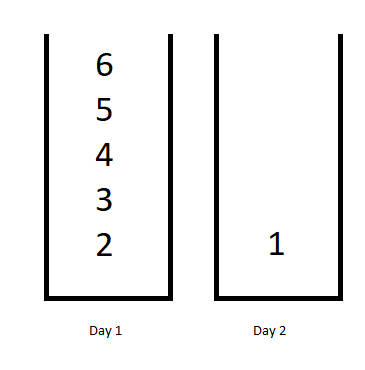
Input: jobDifficulty = [6,5,4,3,2,1], d = 2
Output: 7
Explanation: First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7 

Example 2:

Input: jobDifficulty = [9,9,9], d = 4
Output: -1
Explanation: If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.

Example 3:

Input: jobDifficulty = [1,1,1], d = 3
Output: 3
Explanation: The schedule is one job per day. total difficulty will be 3.

Example 4:

Input: jobDifficulty = [7,1,7,1,7,1], d = 3
Output: 15

Example 5:

Input: jobDifficulty = [11,111,22,222,33,333,44,444], d = 6
Output: 843

Constraints:

• 1 <= jobDifficulty.length <= 300
• 0 <= jobDifficulty[i] <= 1000
• 1 <= d <= 10

思路：

题目意思是给定一个数组，每个元素代表一个任务的完成时间，再给出一个天数，让分配这些任务，每天完成的任务数不限制，耗时按照最大的计算，保证所有天数加起来耗时最小。
可以从划分的角度考虑，对于j个任务，第k天完成的任务的最小值，等于前j-k天完成的最小值，加上后面任务完成所需的最大值。那状态转移方程就可以是: dp[i][k] = min(dp[j][k-1] + max(jobs[j+1, i])) (k - 1 <= j < i)。j个任务的取值范围有下界是因为任务数量一定要大于天数，不然题目是无解的。

代码：

golang:

func minDifficulty(jobs []int, d int) int {
    m := len(jobs)
    if m < d {
        return -1
    }
    
    var dp = make([][]int, m + 1)
    for i := range dp {
        dp[i] = make([]int, d + 1)
        for j := range dp[i] {
            dp[i][j] = math.MaxInt16
        }
    }
    
    dp[0][0] = 0
    for i := 1; i <= m; i++ {
        for k := 1; k <= d; k++ {
            maxDay := 0
            for j := i - 1; j >= k - 1; j-- {
                maxDay = max(maxDay, jobs[j])
                dp[i][k] = min(dp[i][k], dp[j][k-1] + maxDay)
            } 
        }
    }
    
    return dp[m][d]
    
}

func max(i, j int) int {
    if i > j {
        return i
    }
    return j
}

func min(i, j int) int {
    if i < j {
        return i
    }
    return j
}